Es una rama de las matematicas cuyo significado etimologico es la "medicion de los triangulos", en terminos generales, la trigonometria es el estudio de las razones trigonometricas: seno, coseno, secante, cosecante, tangente, cotangente.
Temas vistos durante la clase
Ángulos
El ángulo puede ser definido como la parte del plano determinada por dos semirrectas llamadas lados que tienen el mismo punto de origen llamado vértice del ángulo.La medida de un ángulo es considerada como la longitud del arco de circunferencia centrada en el vértice y delimitada por sus lados.

2. Clases de ángulos

3. Medicion de angulos
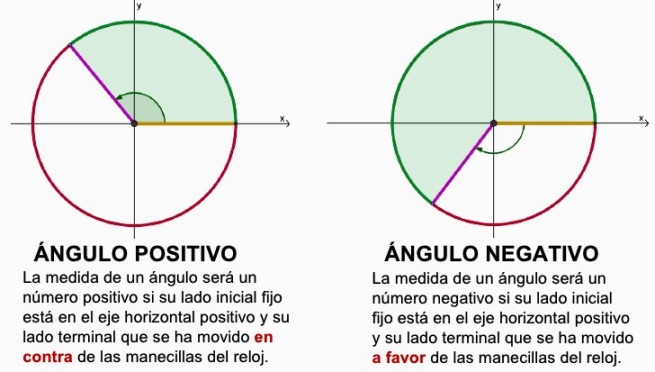
Para medir la amplitud de un ángulo se utiliza un arco de circunferencia con centro en el origen de las semirrectas, si se mide un ángulo en sentido contrario al sentido de giro de las agujas del reloj, se considera positivo. Si se mide en el sentido de giro de las agujas del reloj, se considera negativo.
4. Razones trigonométricas
El ángulo puede ser definido como la parte del plano determinada por dos semirrectas llamadas lados que tienen el mismo punto de origen llamado vértice del ángulo.La medida de un ángulo es considerada como la longitud del arco de circunferencia centrada en el vértice y delimitada por sus lados.

2. Clases de ángulos
Hay varios tipos según su tamaño:
- Ángulo agudo: Mide menos de 90° y más de 0 °.
- Ángulo recto: Mide 90° y sus lados son siempre perpendiculares entre sí.
- Ángulo obtuso: Mayor que 90° pero menor que 180°.
- Ángulo llano: Mide 180°. Igual que si juntamos dos ángulos rectos.
Con una imagen lo verás más fácil.
Todo ángulo comprendido en la zona rosa es un ángulo agudo, y todo ángulo comprendido en la zona azul es un ángulo obtuso.

Para medir la amplitud de un ángulo se utiliza un arco de circunferencia con centro en el origen de las semirrectas, si se mide un ángulo en sentido contrario al sentido de giro de las agujas del reloj, se considera positivo. Si se mide en el sentido de giro de las agujas del reloj, se considera negativo.

4. Razones trigonométricas
Las razones trigonométricas de un ángulo agudo son, básicamente, el seno, el coseno y la tangente. Se definen a partir de un ángulo agudo, , de un triángulo rectángulo, cuyos elementos son la hipotenusa, h, el cateto contiguo al ángulo, , y el cateto opuesto al ángulo, :
- El seno del ángulo es el cateto opuesto dividido por la hipotenusa.
- El coseno del ángulo es el cateto contiguo dividido por la hipotenusa.
- La tangente del ángulo es el cateto opuesto divido por el cateto contiguo o, lo que es lo mismo, el seno del ángulo dividido por el coseno del ángulo.
Existen otras razones trigonométricas derivadas de las anteriores:
- La secante, que es la inversa del coseno: .
- La cosecante, que es la inversa del seno: .
- La cotangente, que es la inversa de la tangente: .
5. Solucion de triangulos
Para resolver un triángulo rectángulo es necesario encontrar los lados y los ángulos que se desconocen a través de los ya conocidos.
Para resolver triángulos rectángulos tendremos en cuenta que:
- La suma de los dos ángulos agudos es 90º.
- La suma de dos lados siempre es mayor que el otro lado.
- Sus lados están relacionados entre sí a través del teorema de Pitágoras:

- Los lados y los ángulos se relacionan entre sí a través de las definiciones de las razones trigonométricas.
Qué datos se necesitan para resolver un triángulo rectángulo
- En general, para poder resolver un triángulo necesitamos conocer como mínimo, un lado, puesto que si conociésemos los ángulos y ningún lado, tendríamos infinitos triángulos semejantes.
- En el caso de los triángulos rectángulos, ya se conoce la medida del ángulo de 90º.
Teniendo en cuenta esto, podemos encontrarnos con dos casos:
- Si se conocen un lado y un ángulo agudo, las razones trigonométricas nos permitirán hallar los otros dos lados.
- Si se conocen dos lados, no necesitamos conocer ningún ángulo puesto que aplicando el teorema de Pitágoras podremos hallar el tercer lado. Y a partir de los lados, se calculan las razones y con éstas, los ángulos.
Es decir, para resolver un triángulo rectángulo, se necesitan dos datos y uno de ellos ha de ser obligatoriamente un lado.
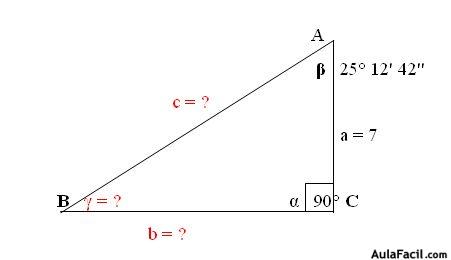
6. Problemas de aplicación
Un problema matemático es una incógnita acerca de una cierta entidad matemática que debe resolverse a partir de otra entidad del mismo tipo que hay que descubrir. Para resolver un problema de esta clase, se deben completar ciertos pasos que permitan llegar a la respuesta y que sirvan como demostración del razonamiento.
7. Funciones trigonométricas
En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.
Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo, asociado a sus ángulos.
8. Caracteristicas
7. Funciones trigonométricas
En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.
Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo, asociado a sus ángulos.
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sen, sin | |
| Coseno | cos | |
| Tangente | tan, tg | |
| Cotangente | ctg (cot) | |
| Secante | sec | |
| Cosecante | csc (cosec) |
8. Caracteristicas
Como características importantes y distintivas de las funciones trigonométricas pueden resaltarse las siguientes:
- Las funciones seno, coseno y tangente son de naturaleza periódica, de manera que el periodo de las funciones seno y coseno es 2p y el de la función tangente es p.
- Las funciones seno y coseno están definidas para todo el conjunto de los números reales. Ambas son funciones continuas (no así la función tangente).
- Las funciones seno y coseno están acotadas (limitadas), ya que sus valores están contenidos en el intervalo [-1,1]. La función tangente no está acotada.
- Las funciones seno y tangente son simétricas respecto al origen, ya que sen (-x) = -sen x; tg (-x)=-tg x. En cambio, la función coseno es simétrica respecto al eje Y: cos (-x) = cos x.
- La gráfica de la función seno

el dominio de la función y = sin x es todos los números reales (el seno está definido para cualquier medida de ángulo), el rango es −1 ≤ y ≤ 1.
La gráfica de la función coseno
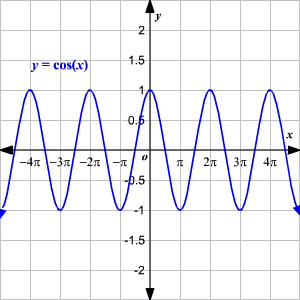
El dominio de la función y = cos x es todos los números reales (el coseno está definido para cualquier medida de ángulo), el rango es −1 ≤ y ≤ 1.
La gráfica de la función tangente

El dominio de la función y = tan x es todos los números reales except o los valores donde el cos x es igual a 0, esto es, los valores  para todos los enteros n . El rango de la función tangente es todos los números reales.
para todos los enteros n . El rango de la función tangente es todos los números reales.
 para todos los enteros n . El rango de la función tangente es todos los números reales.
para todos los enteros n . El rango de la función tangente es todos los números reales.
La gráfica de la función secante

El dominio de la función  es otra vez todos los números reales excepto los valores donde el cos x es igual a 0, esto es, los valores
es otra vez todos los números reales excepto los valores donde el cos x es igual a 0, esto es, los valores  para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
 es otra vez todos los números reales excepto los valores donde el cos x es igual a 0, esto es, los valores
es otra vez todos los números reales excepto los valores donde el cos x es igual a 0, esto es, los valores  para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
La gráfica de la función cosecante

El dominio de la función  es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
 es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
La gráfica de la función cotangente

El dominio de la función  es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es todos los números reales.
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es todos los números reales.
 es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es todos los números reales.
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πn para todos los enteros n . El rango de la función es todos los números reales.
10. Solución de triángulos no rectángulos.
Consiste en determinar las dimensiones características de un triángulo, cuando algunos de estos datos son conocidos. El triángulo se encuentra en un plano o en una esfera.
Para todos los casos en el plano, se debe especificar al menos la longitud de uno de los lados. Si solo se dan los ángulos, no es posible determinar las longitudes de los lados, ya que cualquier triángulo semejante es una solución del problema.
Se pueden resolver con los siguientes teoremas.
11. Teorema de seno
es una proporción entre las longitudes de los lados de un triángulo y los senos de sus correspondientes ángulos opuestos. Usualmente se presenta de la siguiente forma:
relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados:
Son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones, como:
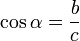
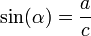
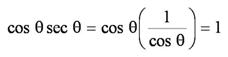
14. Geometría analítica
estudia con profundidad las figuras, sus distancias, sus áreas, puntos de intersección, ángulos de inclinación, puntos de división, volúmenes, etc. Es un estudio más profundo para saber con detalle todos los datos que tienen las figuras geométricas.

15. Recta
recta o la línea recta es una línea que se extiende en una misma dirección; por lo tanto, tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.
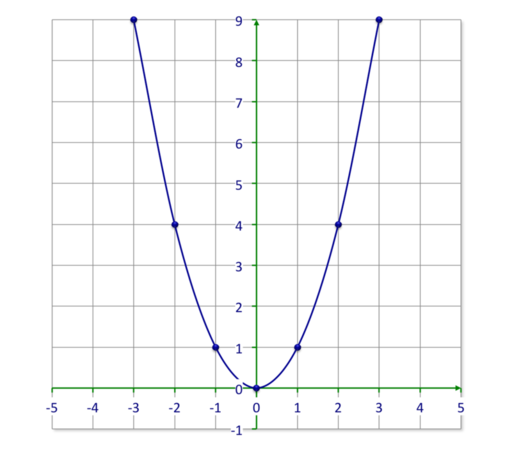
16. Parábola
una parábola es la sección cónica de excentricidad igual a 1, resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.
17. Circunferencia
La circunferencia es una curva plana y cerrada tal que todos sus puntos están a igual distancia del centro.Distíngase de círculo, cuyo lugar geométrico que queda determinado por una circunferencia y la región del plano que encierra esta.

18. Elipse
La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos, llamados focos, es constante.

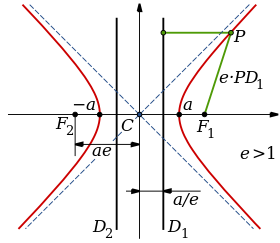
19. Hiperbole
Es una curva abierta de dos ramas obtenida cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución. En geometría analítica, una hipérbola es el lugar geométrico de los puntos de un plano, tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.
20. Ecuaciones trigonométricas
Una ecuación trigonométrica es una ecuación que contiene expresiones trigonométricas y se resuleven usando técnicas similares a las usadas en ecuaciones algebraicas, por lo que las soluciones representaran ángulos.
Por ejemplo las siguientes son ecuaciones trigonométricas:
¿Con que carreras se relaciona?
Consiste en determinar las dimensiones características de un triángulo, cuando algunos de estos datos son conocidos. El triángulo se encuentra en un plano o en una esfera.
Para todos los casos en el plano, se debe especificar al menos la longitud de uno de los lados. Si solo se dan los ángulos, no es posible determinar las longitudes de los lados, ya que cualquier triángulo semejante es una solución del problema.
Se pueden resolver con los siguientes teoremas.
11. Teorema de seno
es una proporción entre las longitudes de los lados de un triángulo y los senos de sus correspondientes ángulos opuestos. Usualmente se presenta de la siguiente forma:
Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son respectivamente a, b, c, entonces:
12. Teorema de coseno
relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados:
Dado un triángulo ABC cualquiera, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:
13. Identidades trigonométricas
Son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones, como:
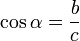
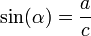
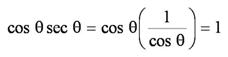
14. Geometría analítica
estudia con profundidad las figuras, sus distancias, sus áreas, puntos de intersección, ángulos de inclinación, puntos de división, volúmenes, etc. Es un estudio más profundo para saber con detalle todos los datos que tienen las figuras geométricas.

15. Recta
recta o la línea recta es una línea que se extiende en una misma dirección; por lo tanto, tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.
16. Parábola
una parábola es la sección cónica de excentricidad igual a 1, resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.

17. Circunferencia
La circunferencia es una curva plana y cerrada tal que todos sus puntos están a igual distancia del centro.Distíngase de círculo, cuyo lugar geométrico que queda determinado por una circunferencia y la región del plano que encierra esta.
18. Elipse
La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos, llamados focos, es constante.
19. Hiperbole
Es una curva abierta de dos ramas obtenida cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución. En geometría analítica, una hipérbola es el lugar geométrico de los puntos de un plano, tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.

20. Ecuaciones trigonométricas
Una ecuación trigonométrica es una ecuación que contiene expresiones trigonométricas y se resuleven usando técnicas similares a las usadas en ecuaciones algebraicas, por lo que las soluciones representaran ángulos.
Por ejemplo las siguientes son ecuaciones trigonométricas:
-
sen (x) = 1 -
π 3 x) = 5 -
2 (2 x − 1) = 0
¿Con que carreras se relaciona?











No hay comentarios:
Publicar un comentario